※ 분류 classification
- regression : Mse(Mean Square Error) : mean(square(Y:정답 - h:예측))
- classification : Cross Entropy: Y * log(h), Y=(0, 1)
* 머신러닝에 필요한 소양 3가지
- 프로그래밍
- 알고리즘
- 수학
import numpy as np# np.log10(10) / 해석 : 10은 log10의 1승이다.
np.log10(0), np.log10(0.001), np.log10(10), np.log10(100), np.log10(1000)→ (-inf, -3.0, 1.0, 2.0, 3.0)
2**2, 2**3, 2**4→ (4, 8, 16)
2**-1, 2**-2, 2**-3, 2**-4→ (0.5, 0.25, 0.125, 0.0625)
np.log(1), np.log(2.71), np.log(5)
# log()는 ()앞에 e라는 수가 숨겨져 있다. e=2.71→ (0.0, 0.99694863489160956, 1.6094379124341003)
x = np.arange(0.00001, 1, 0.0001)
y = np.log(x)
len(x)→ 10000
import matplotlib.pyplot as plt
%matplotlib inlineplt.scatter(x, y)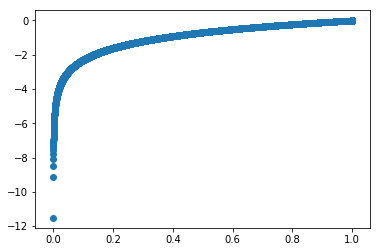
→ classification : Cross Entropy: - (Y log(h) + (1-Y) log(1-h)), Y=(0, 1)
Y = [0, 1, 0] # 정답
h = [0.01, 0.9, 0.7] # 예측
y = np.array(Y)
h = np.array(h)mae = np.mean(np.abs(y - h)) # MAE (평균 절대값 오차)
mse = np.mean(np.square(y - h)) # MSE (평균 제곱 오차)
ce = np.mean(-(y * np.log(h) + (1-y) * np.log(1-h))) # 크로스 엔트로피
mae, mse, ce→ (0.26999999999999996, 0.16669999999999996, 0.43979455194575451)
y * np.log(h) # y = 1인 테이터의 오차→ array([-0. , -0.10536052, -0. ])
(1-y) * np.log(1-h) # y = 0인 데이터의 오차→ array([-0.01005034, -0. , -1.2039728 ])
y = np.array([0, 0, 0, 1, 1, 1])
h = np.array([0.001, 0.1, 0.9, 0.99999, 0.9, 0.3])
np.set_printoptions(precision=3, suppress=True)# (y=1의 오차) + (y=0의 오차)
-(y * np.log(h) + (1-y) * np.log(1-h))→ array([ 0.001, 0.105, 2.303, 0. , 0.105, 1.204])
* 코로나 바이러스 / 분류 / "바이러스가 있냐(1) 없냐(0)
- 증상 : 발열
- 기침(분당 횟수)
- 두통 정도(0:정상 ~ 10:아프다)
- 중국방문여부 (1:방문, 0:없음)
x = [[39, 3, 3, 0], [39, 5, 7, 1], [36.5, 0, 7, 0], [38, 10, 2, 0], [36.6, 2, 2, 0]]
y = [0,1,0,1,0]
x_test = [[38,5,1,0], [37, 10, 5, 1]]* logistic regression 모델을 사용해서 위 데이터를 학습시키고 테스트셋을 예측하세요
* keras로 위 데이터를 학습시 키고 테스트셋을 예측하라
from sklearn.neural_network import MLPClassifier# min max 정규화 [0~1]
# [1,2,3] > [0, 0.5, 1] 최소값 0, 최대값 1이 되도록 변경
# [1,2,3] - 1(최소값) = [0,1,2] / 2(최대값-최소값) = [0, 0.5, 1.0]
x = np.array(x)
x_norm = (x - np.min(x, axis=0)) / (np.max(x, axis=0)-np.min(x, axis=0))
x_norm_test = (x_test - np.min(x, axis=0)) / (np.max(x, axis=0)- np.min(x, axis=0))
x_norm→ array([[ 1. , 0.3 , 0.2 , 0. ], [ 1. , 0.5 , 1. , 1. ], [ 0. , 0. , 1. , 0. ], [ 0.6 , 1. , 0. , 0. ], [ 0.04, 0.2 , 0. , 0. ]])
y→ [0, 1, 0, 1, 0]
# Multi Layer Perceptron 분류기
model = MLPClassifier(max_iter=500).fit(x_norm, y)
model.predict(x_norm), model.predict(x_norm_test)→ (array([0, 1, 0, 1, 0]), array([0, 1]))
* 붓꽃 데이터 받아서 클래스 0.1만 가지고(150개중 100개) MLP로 학습시켜 보세요
from sklearn.linear_model import LogisticRegressionmodel = LogisticRegression().fit(x_norm,y)
model.predict(x)→ array([0, 1, 0, 1, 0])
model.predict(x_test)→ array([0, 1])
model.predict_proba(x)→ array([[ 0.892, 0.108], [ 0.187, 0.813], [ 0.925, 0.075], [ 0.031, 0.969], [ 0.953, 0.047]])
# 해석 : 발열, 기침, 두통, 중국방문
model.coef_, model.intercept_→ (array([[-0.151, 0.833, 0.432, 0.187]]), array([-0.011]))
def sigmoid(x): # 점수 score -> 확률 probability(합이 1) 로 변환
return 1 / (1+np.exp(-x)) # sigmoid를 사용하면 0~1사이 값을 구할 수 있다.# y = sigmoid(WX + b)
sigmoid(np.sum(model.coef_ * x, axis=1) + model.intercept_)성능 지표
- 정확도 accuracy : 정답과 예측의 동일한 비율 (0, 1중에 1샘플이 적은 경우 사용하지 않습니다 : 대부분이 1이 훨씬 적기 때문)
- precision 정밀도, recall 재현율
y = [0,0,0,0,0,0,0,0,1,1] # 정답
h = [0,0,0,0,0,1,1,1,1,1] # 예측from sklearn.metrics import accuracy_score, confusion_matrix, precision_score, recall_score# 정밀율 : 1이라고 예측한 것(5개)중에 맞은(2개) 비율
# 재현율 : 1중(2개)에 맞춘(2개) 비율
# F1-score : 정밀도와 재현율의 조화 평균
precision_score(y,h), recall_score(y ,h)→ (0.40000000000000002, 1.0)
# 정확도, 정밀도, 재현율 측정해 보세요
y = [0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1,1]
h = [1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1]
accuracy_score(y,h), precision_score (y,h),recall_score(y,h)→ (0.080000000000000002, 0.080000000000000002, 1.0)
accuracy_score(y,h)→ 0.080000000000000002
# y축:정답, x 축:예측
confusion_matrix(y, h) # 혼동 행렬
# 3: y=0 인데 h=1 이라고 잘못 예측한 샘플 → array([[ 0, 23], [ 0, 2]], dtype=int64)
'Deep learning > Code' 카테고리의 다른 글
| Convolution (0) | 2020.01.29 |
|---|---|
| Multi-class (0) | 2020.01.29 |
| 분류 classification (0) | 2020.01.23 |
| 2020_01_23 KNN (0) | 2020.01.23 |
| object_detection_yolo_keras (2) | 2020.01.22 |
