책(밑바닥부터 시작하는 딥러닝 2)

Deep learning/Computer vision(영상처리)

책(밑바닥부터 시작하는 딥러닝 2)

ro_ot ㅣ 2020. 2. 6. 18:32

정리

* 자연어 처리 : 우리가 평소 말하는 언어를 컴퓨터가 이해하도록 만드는 기술

* 브로드캐스팅 :

└ 배열의 모양이 특정 제한 조건을 충족 할때 제한 조건을 완화합니다.

└ 계산을 느리게하는 비효율적인 메모리 사용합니다.

* dot / matmul ?

* 미니배치(minibatch) : 데이터를 작은 그룹으로 나눠 그룹 단위로 반복 학습하는 방식을 미니배치 학습이라 하며,

이때 각각의 그룹을 미니배치라 합니다.

* 순전파 : 입력층에서 출력층으로 향하는 전파

* 역전파 : 데이터(기울기)를 순전파와는 반대 방향으로 전파

* params : 가중치와 편향 같은 매개변수를 담는 리스트(매개변수는 여러개가 있을 수 있으므로 리스트에 보관)

* grads : params에 저장된 각 매개변수에 대응하여, 해당 매개변수의 기울기를 보관하는 리스트

* 추론 : 다중클래스 분류등의 문제에 답을 구하는 작업(1.3신경망의 학습 / p39)

* 기울기 : 벡터의 각 원소에 대한 미분을 정리한 것 (1.3.2 미분과 기울기 / p43)

└ '기울기'는 수학에서 말하는 기울기와 다르게 행렬이나 텐서에 대해서도 미분을 정의합니다.

* 오차역전파법(back-propagation) : 신경망의 기울기를 구하는 방법(1.3.3 연쇄법칙 / p44)

Chapter1 : 신경망 복습

1.1.1 벡터(vector) : 크기와 방향을 가진 양

벡터(vector) : 숫자가 일렬로 늘어선 집합(1차원 배열)
행렬(matrix) : 숫자가 2차원 형태로 늘어선 것(2차원)

1.1.2 벡터의 내적과 행렬의 곱

- 벡터의 내적 : 두벡터에서 대응하는 원소들의 곱을 모두 더한 것이며 직관적으로는

'두 벡터가 얼마나 같은 방향을 향하고 있는가' 를 나타냅니다.

┗ 수식 : X·Y = X1Y1 + X2Y2 + ··· + XnYn

# 벡터의 내적
a = np.array([1, 2, 3])
b = np.array([4, 5, 6])
np.dot(a, b)

- 행렬의 곱 : '왼쪽 행렬의 행벡터'와 '오른쪽 행렬의 열벡터'의 내적(원소별 곱의 합)으로 계산합니다.

# 행렬의 곱
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])
np.matmul(A, B)

- no.dat(x , y)의 인수가 배열일 때 1차원 배열이면 벡터의 내적을 계산, 2차원 배열이면 행렬의 곱 계산합니다.

1.1.3 행렬 형상 확인

└ 행렬이나 벡터를 사용해 계산할 때는 형상(shape)에 주의해야 합니다.

- 형상 확인 : 행렬의 곱에서는 대응하는 차원의 원소 수를 일치 시킨다.

1.2 신경망의 추론

└ 신경망은 간단히 말하면 단순한 '함수'라고 할 수 있습니다. 신경망도 함수처럼 입력을 출력으로 변환합니다.

- 신경망은 구현하려면 입력층(input layer), 출력층(out layer), 은닉층(hidden layer)으로 구현 할수 있습니다.

이때 O는 뉴런이며, 그 사이 연결 화살표를 가중치(Weight)라 하고 각 층에서 이전 뉴런의 값에 영향받지 않은 '정수'는 편향(bias)라고 합니다. 신경망은 인접하는 층의 모든 뉴런과 연결되어 있다는 뜻에서 완전연결계층이라고 합니다.

- 형상확인 : 대응하는 차원의 원소 수가 일치함(편향은 생략)

위의 그림에서 보듯, 행렬의 곱에서는 대응하는 차원의 원소 수가 일치 해야합니다.

- 신경망의 추론이나 학습에서는 다수의 샘플데이터(미니배치*)를 한꺼번에 처리해야합니다. 이렇게 하려면 행렬 x의

행 각각에 샘플 데이터를 하나씩 저장해야 합니다.

※ N개의 샘플 데이터를 미니배치로 처리.

- 형상 확인 : 미니배치 버전의 행렬 곱(편향은 생략)

import numpy as np
w1 = np.random.randn(2, 4)  # 가중치
b1 = np.random.randn(4)     # 편향
x = np.random.randn(10, 2)  # 입력
h = np.matmul(x, w1) + b1

- 이 코드의 마지막 줄에서 편향 b1의 덧셈은 브로드캐스트됩니다. b1의 형상은 (4,)지만 자동으로 (10,4)로 복제됩니다.

- 완전연결계층에 의한 변환은 '선형'변환입니다. 여기에 '비선형' 효과를 부여하는 것이 활성화 함수입니다.

- 시그모이드 함수 : 임의의 실수를 입력받아 0~1사이의 실수를 출력합니다.

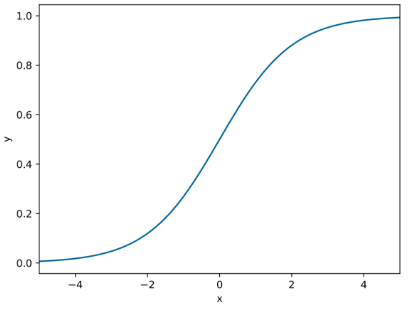
def sigmoid(x):
  return 1/ (1 + np.exp(-x)) # 시그모이드 함수

a = sigmoid(h) # 시그모이드 함수에 의한 비선형 변환

※ 종합

import numpy as np

def sigmoid(x):				
  return 1 / (1+np.exp(-x)) # 시그모이드 함수

x = np.random.randn(10, 2)
w1 = np.random.randn(2, 4)
b1 = np.random.randn(4)
w2 = np.random.randn(4, 3)

b2 = np.random.randn(3)

h = np.matmul(x, w1) + b1
a = sigmoid(h)

s = np.matmul(a, w2) + b2

여기에서 x의 형상은 (10,2)이고 2차우너 데이터 10개가 미니배치로 처리된다는 뜻입니다. 최종 출력인 s의 형상은(10,3)이 됩니다. 이것은 10개의 데이터가 한꺼번에 처리되었고, 각 데이터는 3차원 데이터로 변환되었다는 뜻입니다.

이 신경만은 3차원 데이터를 출력합니다. 따라서 각 차원의 값을 이용하여 3 클래스 분류를 할 수 있습니다. 이경우, 출력된 3차원 벡터의 각 차원은 각 클래스에 대응하는 '점수score'가 됩니다.

▶ 점수란 '확률'이 되기 전의 값입니다. 점수가 높을수록 그 뉴런에 해당하는 클래스의 확률도 높아집니다.

1.2.2 계층으로 클래스화 및 순전파 구현

※ 가정

Affine계층 : 완전연결계층에 의한 변환
Sigmoid계층 : 시그모이드 함수에 의한 변환
파이썬 클래스로 구현
변환 수행 메서드 = forward()

※ 구현규칙

모든 계층은 forward()와 backward() 메서드를 가진다.
모든 계층은 인스턴스 변수인 params와 grads를 가진다.

※ Sigmoid 계층 구현

import numpy as np


class Sigmoid:
    def __init__(self):
        self.params = []

    def forward(self, x):
        return 1 / (1 + np.exp(-x))

- 주 변환 처리 : forward(x)

- Sigmoid는 학습하는 매개변수가 따로 없어 인스턴스 변수인params는 빈 리스트로 초기화 합니다.

※ Affine 계층 구현

# Affine 계층 구현
class Affine:
    def __init__(self, W, b):
        self.params = [W, b]

    def forward(self, x):
        W, b = self.params
        out = np.dot(x, W) + b
        return out

- 초기화될 때 가중치와 편향을 받습니다.

- 가중치와 편향은 Affine 계층의 매개변수이며, 리스트인 params 인스턴스 변수에 보관합니다.

▶ 예제 코드는 앞의 '구현 규칙'을 따르므로, 모든 게층에는 학습해야 하는 매개변수가 반드시 인스턴스 변수인 params에 존재하게

됩니다.

※ TwoLayerNet 구현

└ TwoLayerNet이라는 클래스로 추상화 하고, 주 추론 처리는 predict(x) 메서드로 구현

class TwoLayerNet:
    def __init__(self, input_size, hidden_size, output_size):
        I, H, O = input_size, hidden_size, output_size

        # 가중치와 편향 초기화
        W1 = np.random.randn(I, H)
        b1 = np.random.randn(H)
        W2 = np.random.randn(H, O)
        b2 = np.random.randn(O)

        # 계층 생성
        self.layers = [
            Affine(W1, b1),
            Sigmoid(),
            Affine(W2, b2)
        ]

        # 모든 가중치를 리스트에 모은다.
        self.params = []
        for layer in self.layers:
            self.params += layer.params

    def predict(self, x):
        for layer in self.layers:
            x = layer.forward(x)
        return x

- 초기화 메서드(__init__)는 먼저 가중치를 초기화 하고 3개의 계층을 생성합니다.

- 학습해야 할 가중치 매개변수들을 params 리스트에 저장합니다.

- 모든 계층은 자신의 학습 매개변수들을 인스턴스 변수인 params에 보관하고 있으므로, 이 변수들을 더해줍니다.

- end : TwoLayerNet의 params 변수에는 모든 학습 매개변수가 담기게 되었습니다.

※ TwoLayerNet 클래스를 이용해 신경망의 추론 수행

x = np.random.randn(10, 2)
model = TwoLayerNet(2, 4, 3)
s = model.predict(x)
print(s)

- 이상으로 입력 데이터 x에 대한 점수(s)를 구할 수 있습니다.

1.3 신경망의 학습

└ 최적의 매개 변수 값을 찾는 작업

- 척도 : 신경망 학습에서 학습이 얼마나 잘 되고 있는지를 알기 위함.

└ 손실(loss) : 일반적으로 학습 단계의 특정 시점에서 신경망의 성능을 나타내는 척도로 사용됩니다.

└ 손실은 학습데이터와 신경망이 예측한 결과를 비교하여 예측이 얼마나 나쁜가를 산출한 단일값

- 신경망의 손실은 손실함수(loss function)을 사용합니다.

- 다중 클래스 분류(multi-class classification) 신경망에서는 손실 함수로 교차 엔트로피 오차(CrossEntropy Error)을 사용합니다.

└ 교차 엔트로피 오차는 신경망이 출력하는 각 클래스의 '확률'과 '정답 레이블'을 이용해 구할 수 있습니다.

- X는 입력 데이터, t는 정답 레이블, L은 손실을 나타냅니다. 이때 Softmax 계층의 출력은 확률이 되어, 다음 계층인 Cross Entropy Error 계층에는 확률과 정답 레이블이 입력됩니다.

- 출력이 총 n개일 때, k번째의 출력 yk를 구하는 계산식입니다.

- yk는 k번째 클래스에 해당하는 소프트맥스 함수의 출력입니다.

- 분자는 점수 sk의 지수 함수이고, 분모는 모든 입력 신호의 지수 함수의 총합입니다.

- 출력의 각 원소는 0.0이상 1.0이하의 실수이며 그 원소들을 모두 더하면 1.0이 됩니다.

- tk는 k번째 클래스에 해당하는 정답 레이블이며, log는 네이피어 상수(혹은 오일러의 수) e를 밑으로 하는 로그입니다.

- 정답 레이블은 t = [0, 0, 1]과 같이 원핫 벡터로 표기합니다.

- 데이터는 N개이며, tnk는 n번째 데이터의 k차원째의 값을 의미합니다.

- ynk는 신경망의 출력이고, tnk는 정답 레이블입니다.

1.3.2 미분과 기울기

- 신경망 학습의 목표는 손실을 최소화하는 매개변수를 찾는 것입니다. 이때 중요한 것이 '미분'과 '기울기'입니다.

- L의 W에 대한 기울기를 행렬로 정리할 수 있습니다.

- '행렬과 그 기울기의 형상이 같다'라는 이 성질을 이용하면 매개변수 갱신과 연쇄 법칙을 쉽게 구현 가능합니다.

1.3.3 연쇄 법칙

- 신경망은 학습 데이터를 주면 손실을 출력하고, 이때 매개변수를 갱신하기 위해 각 매개 변수에 대한 손실의 기울기를 얻습니다.

- 오차역전파법을 활용하여 신경망의 기울기를 구합니다.

- 연쇄 법칙은 오차역전파법을 이해하는 열괴이며, 합성함수에 대한 미분의 법칙입니다.( 합성함수란 여러 함수로 구성된 함수)

- 예를 들어, y = f(x)와 z = g(y)라는 두함수가 있을때, z = g(f(x))가 되어 최종 출력 z는 두 함수를 조합해 계산할 수 있습니다.

- 이때 이 합성함수의 미분은 다음과 같이 구할 수 있습니다.

- 위 식이 말하듯, x에 대한 z의 미분은 y = f(x)의 미분과 z = g(y)의 미분을 곱하면 구해지는데 이를 연쇄 법칙이라 합니다.

- 연쇄법칙이 중요한 이유는 아무리 많은 함수를 연결하더라도 그 미분은 개별함수의 미분들을 이용해 구할 수 있기 때문입니다.

▶ 신경망은 여러 '함수'가 연결된 것이라고 생각할 수 있습니다.
오차역전파법은 그 여러 함수(신경망)에 대해 연쇄 법칙을 효율적으로 적용하여 기울기를 구해냅니다.

1.3.4 계산 그래프

계산을 시각적으로 파악할 수 있습니다.
기울기도 직관적으로 구할 수 있습니다.

- 계산 그래프는 노드와 화살표로 그립니다.

- 이때 처리 결과가 순서대로 흐릅니다. 이것이 계산 그래프의 '순전파' 입니다.

- 여기서 중요한 점은 기울기가 순전파와 반대 방향으로 전파되는데 이 반대 방향의 전파가 '역전파'입니다.

- 우리 목표는 L의 미분(기울기)을 각 변수에 대해 구하는 것입니다.

- 이때 전파되는 값은 최종 출령 L의 각 변수에 대한 미분입니다.

- z에 대한 미분은 ∂L/∂z이고, x와 y에 대한 미분은 각각 ∂L/∂x과 ∂L/∂y입니다.

- 연쇄법칙에 따르면 역전파로 흐르는 미분값은 상류로부터 흘러온 미분과 각 연산노드의 미분을 곱해 계산 가능합니다.

그러므로 이 예에서는 ∂L/∂x=∂L/∂z*∂z/∂x이고, ∂L/∂y=∂L/∂z*∂z/∂y가 됩니다.

따라서 ∂z/∂x=1과 ∂z/∂y=1이라는 결과를 구할 수 있습니다.

- 계산 그래프를 구축하는 연산 노드로는 여기서 본 '덧셈노드' 외에도 다양한 연산을 생각할 수 있습니다.

※ 곱셈 노드

곱셈노드의 역전파는 아래 그림처럼 '상류로부터 받은 기울기'에 '순전파 시의 입력을 서로 바꾼 값'을 곱합니다.

(즉, 순전파 시 입력이 x면 y를 곱하고, y면 x를 곱합니다.)

* 벡터나 행렬 혹은 텐서 같은 다변수를 흘려도 문제 없습니다.

└ 텐서의 다른 원소들과는 독립적으로, '원소별 연산'을 수행합니다.

※ 분기 노드

분기 노드는 따로 그리지 않고 단순이 선 2개로 나뉘도록 그리는데 이때 값이 복제되어 분기합니다.(복제노드라고도 함)

(역전파는 상류에서 온 기울기들의 '합')

※ Repeat 노드

2개로 분기하는 분기 노드를 일반화하면 N개로의 분기(복제)가 되는데 이를 Repeat노드라고 합니다.

* 길이가 D인 배열을 N개로 복제하는 예이며 이 Repeat노드는 N개의 분기노드로 볼수 있습니다.

(역전파는 N개의 기울기를 모두 더해 구할 수 있습니다.)

import numpy as np
D, N = 8, 7
x = np.random.randn(1, D)                # 입력
y = np.repeat(x, N, axis=0)              # 순전파
dy = np.random.randn(N, D)               # 무작위 기울기
dx = np.sum(dy, axis=0, keepdims=True)   # 역전파

* np.repeat()메서드가 원소복제를 수행합니다. 이때 axis를 지정하여 어느 축 방향으로 복제할지를 조정할 수 있습니다.

* np.sum()역전파에서는 총합을 구해야 하므로 이용합니다. 이때도 axis인수를 설정하여 어느 축 방향으로

합을 구할지 지정합니다.

* keepdims=True를 설정하여 2차원 배열의 차원 수를 유지합니다.

└ 이 예에서 keepdims가 True면 np.sum()의 결과의 형상은 (1,N)이 되며, False면 (N, )이 됩니다.

▶ 넘파이의 브로드캐스트는 배열의 원소를 복제하며 Repeat 노드를 사용하여 이 기능을 표현할 수 있습니다.

※ Sum 노드

Sum노드는 범용 덧셈 노드입니다.

* Sum 노드의 역전파는 상류로부터의 기울기를 모든 화살표에 분배합니다.(덧셈 노드의 역전파를 확장한 것)

import numpy as np
D, N = 8, 7
x = np.random.randn(N, D)             # 입력
y = np.sum(x, axis=0, keepdims=True)  # 순전파
dy = np.random.randn(1, D)            # 무작위 기울기
dx = np.repeat(dy, N, axis = 0)       # 역전파

Sum노드의 순전파는 np.sum() 메서드로, 역전파는 np.repeat()메서드로 구현 할 수 있습니다.

(Sum노드와 Repeat노드는 서로 '반대 관계' 인 것을 볼수있습니다.)

※ MatMul 노드('Matrix Multiplay'의 약자)

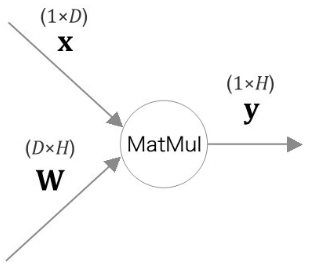
이때 x의 i번째 원소에 대한 미분 ∂L/∂xi은 다음과 같이 구합니다.

이 식의 ∂L/∂xi를 변화시켰을 때 L이 얼마나 변할 것인가라는 '변화의 정도'를 나타냅니다.

여기서 xi를 변화시키면 벡터 y의 모든 원소가 변하고, 그로 인해 최종적으로 L이 변하게 됩니다.

따라서 xi에서 L에 이르는 연쇄 법칙경로는 여러 개가 있으며 그 총합은 ∂L/∂xi이 됩니다.

1.3.5 기울기 도출과 역전파 구현

- 계산 그래프 설명도 끝났으니 이어서 실용적인 계층을 구현

( Sigmoid계층, 완전연결계층의 Affine 계층, Softmax with Loss 계층을 구현)

※ Sigmoid 계층

- 시그모이드 함수를 수식으로 쓰면 y= 1/ 1+exp(-x)입니다. 미분은 아래 그림과 같습니다.

- Sigmoid 계층의 계산 그래프를 아래 그림 처럼 그릴 수 있습니다.

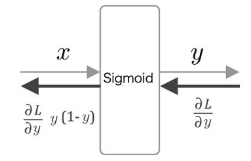
- 출력 쪽 계층으로부터 전해진 기울기 (∂L/∂y)에 시그모이드 함수의 미분 (∂y/∂x),즉y(1-y)를 곱하고,

그 값을 입력 쪽 계층으로 전파합니다.

class MatMul:
  def __init__(self):
    self.params, self.grads = [], []
    self.out = None

  def forword(self, x):
    out = 1 / (1+np.exp(-x))
    self.out = out
    return out
    
  def backward(self, dout):
    dx = dout * (1.0 - self.out) * self.out
    return dx

- 순전파 때는 출력을 인스턴스 변수 out에 저장하고, 역전파를 계산할 때 이 out 변수를 사용하는 모습을 볼 수 있다.

※ Affine 계층

- Affine 계층의 순전파는 y = np.matmul(x, W) + b로 구현할 수 있습니다.

- 여기서 편향을 더할 때는 넘파이의 브로드캐스트가 사용됩니다.

- 위 그림처럼 MatMul노드로 행렬 곱을 계산하고 편향은 Repeat 노드에 의해 복제된 후 더해집니다.

class MatMul:
  def __init__(self, W, b):
    self.params = [W, b]
    self.grads = [np.zeros_like(W), np.zeros_like(b)]
    self.x = None

  def forword(self, x):
    W, b = self.params
    out = np.matmul(x, W) +b
    self.x = x
    return
    
  def backward(self, dout):
    W, b = self.params
    dx = np.matmul(dout, W.T)
    dW = np.matmul(self.x.T, dout)
    db = np.sum(dout, axis=0)
    self.grads[0][...]=dW
    self.grads[1][...]=db
    return dx

- 인스턴스 변수 params에는 매개변수를, grads에는 기울기를 저장 합니다.

Affine의 역전파는 MatMul 노드와 Repeat노드의 역전파를 수행하면 구할 수 있습니다. Repeat 노드의 역전파는

np.sum() 메서드로 계산할 수 있는데 행렬의 형상을 잘 살펴보고 어느 축으로 합을 구할지를 명시해야 합니다.

마지막으로, 가중치 매개변수의 기울기를 인스턴스 변수 grads에 저장까지 하는게 Affine 계층의 구현입니다.

※ Softmax with Loss 계층

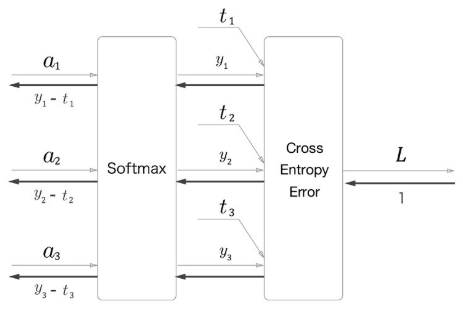
- 3-클래스 분류를 가정하여 이전 계층(입력층에 가까운 계층)으로부터 3개의 입력을 받도록 했습니다.

- Softmax 계층은 입력(a1,a2,a3)를 정규화하여 (y1,y2,y3)를 출력합니다. 그리고 Cross Entropy Error 계층은

Softmax의 출력 (y1,y2,y3)와 정답 레이블(t1,t2,t3)를 받고, 이 데이터로부터 손실 L을 구해 출력합니다.

▶ Softmax계층의 역전파는 (y1-t1, y2-t2, y3-t3)로 깔끔하게 떨어집니다. (y1,y2,y3)는 Softmax 계층의 출력이고, (t1,t2,t3)는 정답 레이블이므로, Softmax 계층의 역전파는 자신의 출력과 정답 레이블의 차이라는 뜻 입니다.

이처럼 신경망의 역전파는 이 차이(오차)를 앞 계층에 전해주는 것으로, 신경망 학습에서 아주 중요한 성질입니다.

1.3.6 가중치 갱신

오차역전파법으로 기울기를 구했으면, 그 기울기를 사용해 신경망의 매개변수를 갱신합니다.

* 신경망의 학습 순서

→ 1단계: 미니배치

훈련 데이터 중에서 무작위로 다수의 데이터를 골라낸다

→ 2단계: 기울기 계산

오차역전파법으로 각 가중치 매개변수에 대한 손실 함수의 기울기를 구한다.

→ 3단계: 매개변수 갱신

기울기를 사용하여 가중치 매개변수를 갱신한다.

→ 4단계: 반복

1~ 3단계를 필요한 만큼 반복한다.

- 오차역전파법으로 가중치의 기울기를 얻을수 있습니다, 이 기울기는 현재의 가중치 매개변수에서 손실을 가장 크게 하는 방향을 가리킵니다. 따라서 매개변수를 기울기와 반대방향으로 갱신하면 손실을 줄일 수 있는데 이를 경사하강법(Gradient Descent)입니다.

- 가중치 갱신 기법의 종류중 가장 단순한 확률적경사하강법(Stochastic Gradient Descent)을 구현합니다.

└ '확률적(Stochastic)'은 무작위로 선택된 데이터(미니배치)에 대한 기울기를 이용한단 뜻

- SGD는 현재의 가중치를 기울기 방향으로 일정한 거리만큼 갱신합니다.

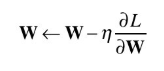
- 위 식에서 갱신하는 가중치 매개변수가 W이고, W에 대한 손실 함수의 기울기가 ∂L/∂W 이며 n에타는 학습률을 나타냅니다. 실제로는 0.01이나 0.001 같은 값을 미리 정하고 사용합니다.

class SGD:
    '''
    확률적 경사하강법(Stochastic Gradient Descent)
    '''
    def __init__(self, lr=0.01):
        self.lr = lr
        
    def update(self, params, grads):
        for i in range(len(params)):
            params[i] -= self.lr * grads[i]

- 초기화 인수 lr은 학습률을 뜻하며, 그 값을 인스턴스 변수로 저장해둡니다.

'Deep learning > Computer vision(영상처리)' 카테고리의 다른 글

책(밑바닥부터 시작하는 딥러닝 2) 4 (0)	2020.02.13
BoW(이미지관련) (0)	2020.02.12
GAN(이론) (0)	2020.02.12
책(밑바닥부터 시작하는 딥러닝 2) 3 (0)	2020.02.11
책(밑바닥부터 시작하는 딥러닝 2) 2 (0)	2020.02.10

정착소